Juliol 2022 – Problema 6
Considerar la funció 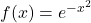 per als valors positius de
per als valors positius de 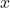 . Per cada punt
. Per cada punt 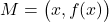 de la gràfica de
de la gràfica de 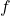 es tracen dues rectes paral·leles als eixos de coordenades
es tracen dues rectes paral·leles als eixos de coordenades 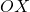 i
i 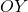 . Aquestes dues rectes, junt
amb els eixos de coordenades, defineixen un rectangle.
. Aquestes dues rectes, junt
amb els eixos de coordenades, defineixen un rectangle.
- Determinar l’àrea del rectàngle en funció de
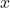 . (3 punts)
. (3 punts) - Trobar el punt
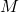 que proporciona major àrea i calcular aquesta àrea. (7 punts)
que proporciona major àrea i calcular aquesta àrea. (7 punts)
Juny 2022 – Problema 6
Es desitja construir un quadrat i un triangle equilàter tallant en dues parts un cable d’acer de 240 metres de longitud.
- Calcular la suma de les àrees del triangle i del quadrat en funció del valor
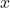 que correspon amb els metres que mesura un costat del triangle. (3 punts)
que correspon amb els metres que mesura un costat del triangle. (3 punts) - Calcular la longitud de cable necessària per a construir el triangle de manera que la suma de les àrees del triangle i del quadrat siga mínima i calcular l’àrea mínima. (7 punts)
Juliol 2021 – Problema 6
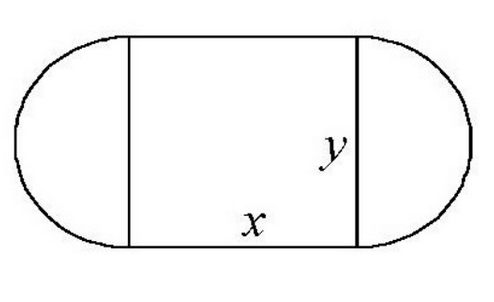
Volem dissenyar un camp de joc de manera que la part central siga rectangular, i les parts laterals siguen semicircumferències cap a fora. La superfície del camp mesura 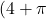 metres quadrats. Es volen pintar totes les ratlles de dit camp
tal i com es mostra en la figura. Es demana:
metres quadrats. Es volen pintar totes les ratlles de dit camp
tal i com es mostra en la figura. Es demana:
- Escriviu la longitud total de les ratlles del camp en funció de l’altura
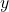 del rectangle. (5 punts)
del rectangle. (5 punts) - Calculeu les dimensions del camp per a que la pintura utilitzada siga mínima. (5 punts)
Juny 2021 – Problema 6
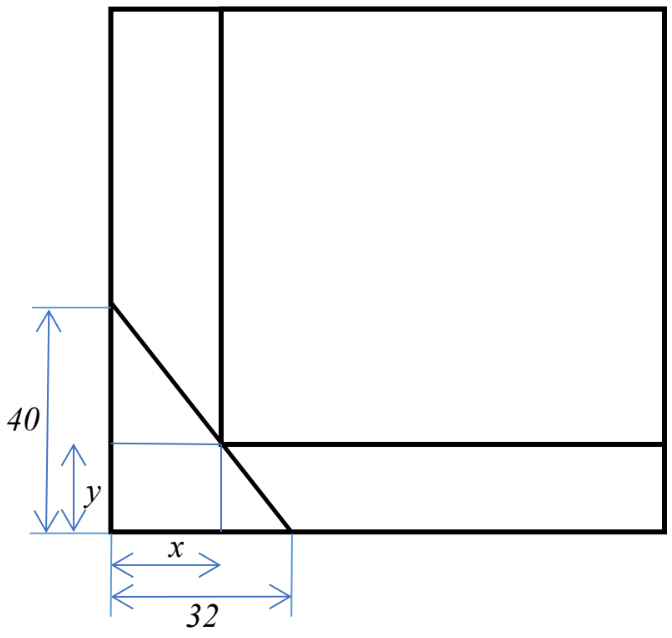
Un espill pla, quadrat, de 80 cm de costat, s’ha trencat per un cantó seguint una línia recta. El tros desprès té forma de triangle rectangle de catets 32 cm i 40 cm respectivament. En l’espill trencat retallem una peça rectangular 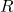 , un dels
vèrtexs de la qual és el punt
, un dels
vèrtexs de la qual és el punt 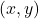 (vegeu la figura).
(vegeu la figura).
- Trobeu l’àrea de la peça rectangular obtinguda com a funció de
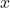 , quan
, quan 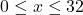 . (4 punts)
. (4 punts) - Calculeu les dimensions que tindrà
 perquè la seua àrea siga màxima. (4 punts)
perquè la seua àrea siga màxima. (4 punts) - Calculeu el valor d’aquesta àrea màxima. (2 punts)
Setembre 2020 – Problema 6
Els vèrtexs d’un triangle són 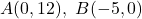 i
i 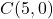 . Es desitja construir un rectangle inscrit en el triangle anterior, de costats paral·lels als eixos coordenats i dos dels dels seus vèrtexs tenen coordenades
. Es desitja construir un rectangle inscrit en el triangle anterior, de costats paral·lels als eixos coordenats i dos dels dels seus vèrtexs tenen coordenades 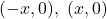 , on
, on 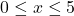 . Els altres dos vèrtexs estan situats als segments
. Els altres dos vèrtexs estan situats als segments 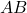 i
i 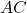 . Obtindre raonadament, escrivint tots els passos del raonament utilitzat:
. Obtindre raonadament, escrivint tots els passos del raonament utilitzat:
- L’expressió
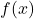 de l’àrea del rectangle anterior. (4 punts)
de l’àrea del rectangle anterior. (4 punts) - El valor d’
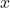 per al que l’àrea és màxima i les dimensions del rectangle obtingut. (3 punts)
per al que l’àrea és màxima i les dimensions del rectangle obtingut. (3 punts) - La proporció entre l’àrea del rectangle anterior i l’àrea del triangle. (3 punts)
Juliol 2020 – Problema 6
En un triangle isòsceles, els dos costats iguals mesuren 10 centímetres cadascun . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- L’expressió de l’àrea
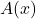 del triangle, en funció de la longitud
del triangle, en funció de la longitud 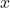 del tercer costat. (4 punts)
del tercer costat. (4 punts) - Els intervals de creixement i decreixement de la funció
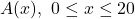 . (4 punts)
. (4 punts) - La longitud
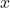 del tercer costat per a que l’àrea del triangle siga màxima i el valor d’aquesta àrea. (2 punts)
del tercer costat per a que l’àrea del triangle siga màxima i el valor d’aquesta àrea. (2 punts)
Encara no disponible
Juliol 2019 – Problema 3.B.
Un projectil està unit al punt 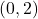 per una corda elàstica i tensa. El projectil recorre la corba
per una corda elàstica i tensa. El projectil recorre la corba 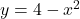 d’extrems
d’extrems 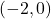 i
i 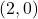 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La funció de la variable
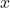 que expressa la distància entre un punt qualsevol
que expressa la distància entre un punt qualsevol 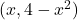 de la corba
de la corba 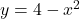 i el punt
i el punt 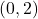 . (2 punts)
. (2 punts) - Els punts de la corba
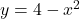 a major distància absoluta del punt
a major distància absoluta del punt 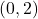 per a
per a 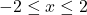 . (2 punts)
. (2 punts) - Els punts de la corba
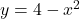 a menor distància absoluta del punt
a menor distància absoluta del punt 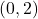 per a
per a 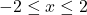 . (2 punts)
. (2 punts) - L’àrea de la superfície per la que s’ha menejat la corda elàstica, és a dir, l’àrea compresa entre les corbes
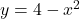 i
i 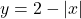 quan
quan 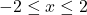 . (4 punts)
. (4 punts)
Juny 2019 – Problema 3.B.
Les coordenades inicials dels mòbils  i
i  són
són 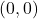 i
i 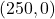 , respectivament, sent 1 km la distància de l’origen de coordenades a cadascun dels punts
, respectivament, sent 1 km la distància de l’origen de coordenades a cadascun dels punts 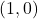 i
i 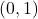 .
.
El mòbil  es desplaça sobre l’eix
es desplaça sobre l’eix 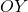 des de la seua posició inicial fins el punt
des de la seua posició inicial fins el punt 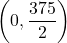 amb una velocitat de 30 km/h i, simultàniament, el mòbil
amb una velocitat de 30 km/h i, simultàniament, el mòbil  es desplaça sobre l’eix
es desplaça sobre l’eix 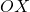 des de la seua
posició inicial fins l’origen de coordenades a una velocitat de 40 km/h.
des de la seua
posició inicial fins l’origen de coordenades a una velocitat de 40 km/h.
Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La distància
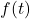 entre els mòbils
entre els mòbils  i
i  durant el desplaçament, en funció del temps
durant el desplaçament, en funció del temps 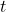 en hores des de que començaren a desplaçar-se. (2 punts)
en hores des de que començaren a desplaçar-se. (2 punts) - El temps
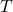 que tarden els mòbils en desplaçar-se des de la seua posició inicial a la seua posició final, i els intervals de creixement i de decreixement de la funció
que tarden els mòbils en desplaçar-se des de la seua posició inicial a la seua posició final, i els intervals de creixement i de decreixement de la funció 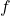 al llarg del trajecte. (4 punts)
al llarg del trajecte. (4 punts) - Els valors de
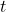 per als que la distància dels mòbils és màxima i mínima durant el seu desplaçament i dites distàncies màxima i mínima. (4 punts)
per als que la distància dels mòbils és màxima i mínima durant el seu desplaçament i dites distàncies màxima i mínima. (4 punts)