Opció A – Problema 1
Es donen la matriu 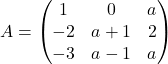 , que depèn del paràmetre
, que depèn del paràmetre  , i una matriu quadrada
, i una matriu quadrada  d’ordre 3 tal que
d’ordre 3 tal que 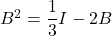 sent
sent 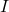 la matriu identitat d’ordre 3. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
la matriu identitat d’ordre 3. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
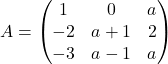 , que depèn del paràmetre
, que depèn del paràmetre - El rang de la matriu
 en funció del paràmetre
en funció del paràmetre  i el determinant de la matriu
i el determinant de la matriu 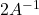 quan
quan 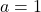 . (2+2 punts)
. (2+2 punts) - Totes les solucions del sistema d’equacions
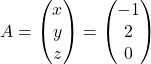 quan
quan 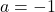 . (3 punts)
. (3 punts) - La comprovació de que
 és invertible, trobant
és invertible, trobant 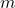 i
i 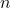 tals que
tals que 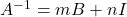 . (3 punts)
. (3 punts)
Opció A – Problema 2
Considerem en l’espai les rectes 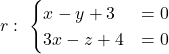 i
i 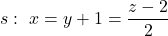 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
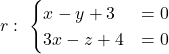 i
i - L’equació del pla que conté les rectes
 i
i  . (3 punts)
. (3 punts) - La recta que passa per
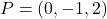 i talla perpendicularment a la recta
i talla perpendicularment a la recta  . (4 punts)
. (4 punts) - El valor que deuen tindre els paràmetres reals
 i
i 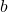 per a que la recta
per a que la recta  estiga continguda en el pla
estiga continguda en el pla 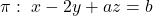 . (3 punts)
. (3 punts)
Opció A – Problema 3
Es considera la funció 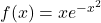 . Obtín raonadament, escrivint tots els passos del raonament utiltizat:
. Obtín raonadament, escrivint tots els passos del raonament utiltizat:
- Les assímptotes, els intervals de creixement i de decreixement, així com els màxims i mínims relatius de la funció
 . (3 punts)
. (3 punts) - La representació gràfica de la corba
 . (2 punts)
. (2 punts) - El valor del paràmetre
 per a que es puga aplicar el teorema de Rolle en l’interval
per a que es puga aplicar el teorema de Rolle en l’interval ![Rendered by QuickLaTeX.com [0,1]](https://matematiques.es/wp-content/ql-cache/quicklatex.com-25b6d943ab489c05a3dbd5ea29087a48_l3.png) a la funció
a la funció 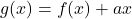 . (1 punt)
. (1 punt) - El valor de les integrals indefinides
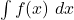 i
i 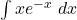 . (4 punts)
. (4 punts)
Opció B – Problema 1
Es té el sistema d’equacions 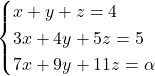 , on
, on  és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat
és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat
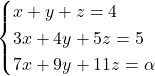 , on
, on - Els valors del paràmetre
 per als que el sistema és compatible i els valors d’
per als que el sistema és compatible i els valors d’ per als que el sistema és incompatible. (4 punts)
per als que el sistema és incompatible. (4 punts) - Totes les solucions del sistema quan siga compatible. (4 punts)
- La discussió de la compatibilitat i determinació del nou sistema deduït de l’anterior al canviar el coeficient 11 per qualsevol altre nombre diferent. (2 punts)
Opció B – Problema 2
Siga  el pla d’equació
el pla d’equació 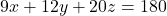 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- Les equacions dels dos plans paral·lels a
 que disten 4 unitats de
que disten 4 unitats de  . (4 punts)
. (4 punts) - Els punts
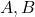 i
i 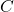 intersecció del pla
intersecció del pla  amb els eixos
amb els eixos 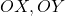 i
i 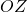 i l’angle que formen els vectors
i l’angle que formen els vectors 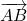 i
i 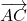 . (4 punts)
. (4 punts) - El volum del tetraedre el qual els seus vèrtexs són l’origen
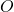 de coordenades i els punts
de coordenades i els punts 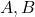 i
i 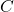 . (2 punts)
. (2 punts)
Encara no disponible.
Opció B – Problema 3
Les coordenades inicials dels mòbils  i
i  són
són 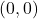 i
i 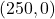 , respectivament, sent 1 km la distància de l’origen de coordenades a cadascun dels punts
, respectivament, sent 1 km la distància de l’origen de coordenades a cadascun dels punts 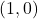 i
i 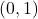 .
.
El mòbil  es desplaça sobre l’eix
es desplaça sobre l’eix 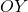 des de la seua posició inicial fins el punt
des de la seua posició inicial fins el punt 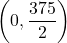 amb una velocitat de 30 km/h i, simultàniament, el mòbil
amb una velocitat de 30 km/h i, simultàniament, el mòbil  es desplaça sobre l’eix
es desplaça sobre l’eix 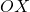 des de la seua
posició inicial fins l’origen de coordenades a una velocitat de 40 km/h.
des de la seua
posició inicial fins l’origen de coordenades a una velocitat de 40 km/h.
Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La distància
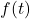 entre els mòbils
entre els mòbils  i
i  durant el desplaçament, en funció del temps
durant el desplaçament, en funció del temps 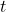 en hores des de que començaren a desplaçar-se. (2 punts)
en hores des de que començaren a desplaçar-se. (2 punts) - El temps
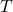 que tarden els mòbils en desplaçar-se des de la seua posició inicial a la seua posició final, i els intervals de creixement i de decreixement de la funció
que tarden els mòbils en desplaçar-se des de la seua posició inicial a la seua posició final, i els intervals de creixement i de decreixement de la funció 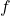 al llarg del trajecte. (4 punts)
al llarg del trajecte. (4 punts) - Els valors de
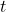 per als que la distància dels mòbils és màxima i mínima durant el seu desplaçament i dites distàncies màxima i mínima. (4 punts)
per als que la distància dels mòbils és màxima i mínima durant el seu desplaçament i dites distàncies màxima i mínima. (4 punts)