En les respostes es deuen escriure tots els passos del raonament utilitzat.
Problema 1
Donat el sistema d’equacions 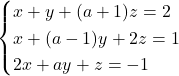 .
.
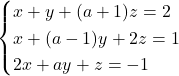 .
.- Estudieu-lo en funció dels valors del paràmetre real
 . (5 punts)
. (5 punts) - Trobeu totes les solucions del sistema quan aquest siga compatible. (5 punts)
Problema 2
Es donen els plans 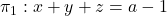 ,
, 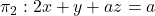 i
i 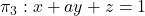 .
.
- Determineu la posició relativa dels tres plans en funció del paràmetre
 . (4 punts)
. (4 punts) - Per a
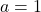 , calculeu, si existeix, la recta de tall entre els plans
, calculeu, si existeix, la recta de tall entre els plans 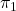 i
i 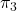 . (3 punts)
. (3 punts) - Per a
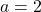 , calculeu, si existeix, la recta de tall entre els plans
, calculeu, si existeix, la recta de tall entre els plans 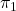 i
i 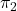 . (3 punts)
. (3 punts)
Encara no disponible.
Problema 3
Considerem la funció 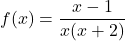 . Obtingau:
. Obtingau:
- El domini i les assímptotes de la funció. (2 punts)
- Els intervals de creixement i de decreixement de
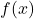 . (4 punts)
. (4 punts) - La integral
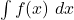 . (4 punts)
. (4 punts)
Problema 4
Donada la matriu 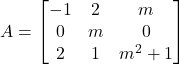 , es demana:
, es demana:
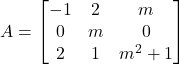 , es demana:
, es demana:- Obtingau el rang de la matriu en funció del paràmetre
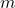 . (4 punts)
. (4 punts) - Expliqueu quan la matriu
 és invertible. (2 punts)
és invertible. (2 punts) - Resoleu l’equació
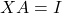 on
on 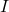 és la matriu identitat en el cas que
és la matriu identitat en el cas que 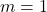 . (4 punts)
. (4 punts)
Problema 5
Donats el punt 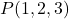 i el pla
i el pla 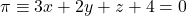 , es demana:
, es demana:
- Calculeu la distància del punt
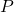 al pla
al pla  . (2 punts)
. (2 punts) - Calculeu el punt
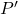 que és simètric del punt
que és simètric del punt 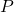 respecte del pla
respecte del pla  . (5 punts)
. (5 punts) - Calculeu l’equació del pla
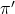 que passa per
que passa per 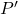 i és paral·lel a
i és paral·lel a  . (3 punts)
. (3 punts)
Encara no disponible.
Problema 6
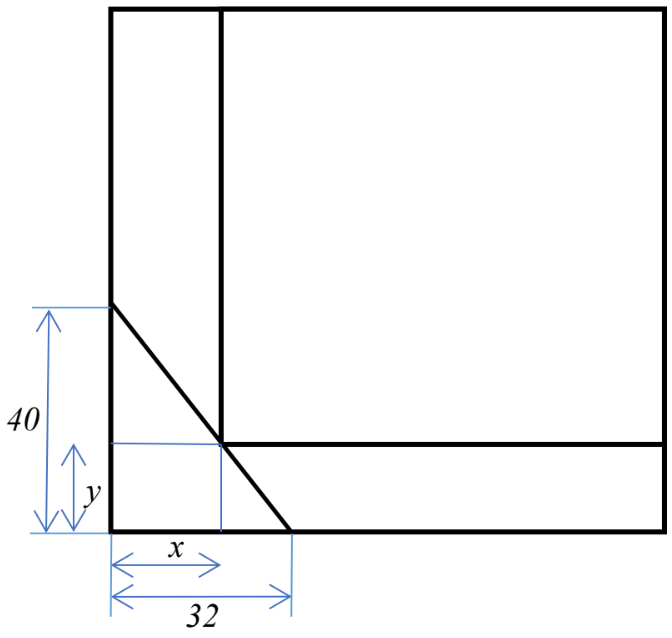
Un espill pla, quadrat, de 80 cm de costat, s’ha trencat per un cantó seguint una línia recta. El tros desprès té forma de triangle rectangle de catets 32 cm i 40 cm respectivament. En l’espill trencat retallem una peça rectangular 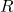 , un dels
vèrtexs de la qual és el punt
, un dels
vèrtexs de la qual és el punt 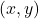 (vegeu la figura).
(vegeu la figura).
- Trobeu l’àrea de la peça rectangular obtinguda com a funció de
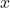 , quan
, quan 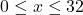 . (4 punts)
. (4 punts) - Calculeu les dimensions que tindrà
 perquè la seua àrea siga màxima. (4 punts)
perquè la seua àrea siga màxima. (4 punts) - Calculeu el valor d’aquesta àrea màxima. (2 punts)