Juliol 2022 – Problema 2
Donada la matriu 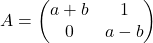 :
:
- Calcular els valors dels paràmetres
 i
i 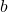 per a que es complisca que
per a que es complisca que 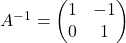 . (4 punts)
. (4 punts) - Per als valors d’
 i
i 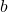 obtinguts en l’apartat anterior, calcular
obtinguts en l’apartat anterior, calcular 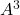 i
i 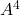 . (3 punts)
. (3 punts) - Calcular
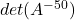 quan
quan 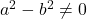 . (3 punts)
. (3 punts)
Juny 2022 – Problema 1
Donades les matrius 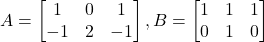 i
i 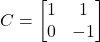 .
Es demana:
.
Es demana:
- Demostrar que
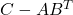 té inversa i calcular-la. (4 punts)
té inversa i calcular-la. (4 punts) - Calcular la matriu
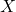 que verifica
que verifica 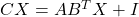 , on
, on 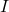 és la matriu identitat. (3 punts)
és la matriu identitat. (3 punts) - Justificar que
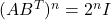 per a tot nombre natural
per a tot nombre natural 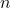 . (3 punts)
. (3 punts)
Juny 2022 – Problema 2
div>Donada la matriu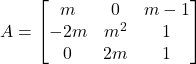 . Determinar:
. Determinar:- El rang de la matriu
 en funció del paràmetre real
en funció del paràmetre real 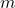 . (4 punts)
. (4 punts) - La matriu inversa d’
 en el cas
en el cas 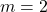 . (4 punts)
. (4 punts) - El nombre real
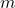 per al que el determinant de la matriu
per al que el determinant de la matriu 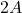 és igual a
és igual a 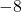 . (2 punts)
. (2 punts)
Juliol 2021 – Problema 4
Es donen les matrius 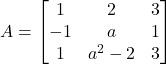 i
i 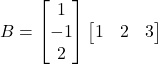 . Obtingau:
. Obtingau:
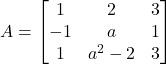 i
i  . Obtingau:
. Obtingau:- El rang de la matriu
 segons els valors del paràmetre
segons els valors del paràmetre  . (3 punts)
. (3 punts) - Una matriu
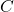 tal que
tal que 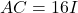 , sent
, sent 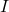 la matriu identitat, quan
la matriu identitat, quan 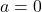 . (4 punts)
. (4 punts) - El rang de la matriu
 i la discussió de si el sistema
i la discussió de si el sistema  té solució. (3 punts)
té solució. (3 punts)
Juny 2021 – Problema 4
Donada la matriu 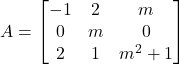 , es demana:
, es demana:
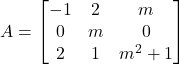 , es demana:
, es demana:- Obtingau el rang de la matriu en funció del paràmetre
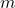 . (4 punts)
. (4 punts) - Expliqueu quan la matriu
 és invertible. (2 punts)
és invertible. (2 punts) - Resoleu l’equació
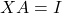 on
on 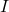 és la matriu identitat en el cas que
és la matriu identitat en el cas que 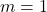 . (4 punts)
. (4 punts)
Setembre 2020 – Problema 4
Siga 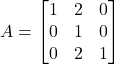 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
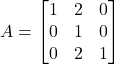 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:- La justificació de que
 té inversa i el càlcul de dita matriu inversa. (3 punts)
té inversa i el càlcul de dita matriu inversa. (3 punts) - Dos constants
 i
i 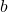 de manera que
de manera que 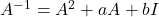 . Es pot utilitzar (sense comprovar-ho) que
. Es pot utilitzar (sense comprovar-ho) que  verifica que
verifica que 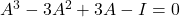 sent
sent 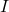 la matriu identitat. (3 punts)
la matriu identitat. (3 punts) - El valor de
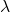 per a que el sistema d’equacions
per a que el sistema d’equacions 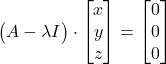 tinga infinites solucions. Per a dit valor de
tinga infinites solucions. Per a dit valor de 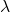 trobar totes les solucions del sistema. (2+2 punts)
trobar totes les solucions del sistema. (2+2 punts)
Juliol 2020 – Problema 4
Es donen les matrius 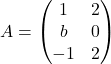 i
i 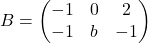 , que depenen del paràmetre real
, que depenen del paràmetre real 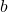 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
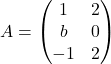 i
i - Els valors de
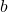 per a que cadascuna de les matrius
per a que cadascuna de les matrius 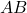 i
i 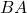 tinguen inversa. (3 punts)
tinguen inversa. (3 punts) - Els valors de
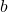 per a que la matriu
per a que la matriu 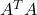 tinga inversa, sent
tinga inversa, sent 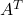 la matriu trasposta d’
la matriu trasposta d’ . (3 punts)
. (3 punts) - La inversa d’
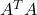 , quan aquesta inversa existisca. (4 punts)
, quan aquesta inversa existisca. (4 punts)
Juliol 2019 – Problema 1.B.
Es donen les matrius 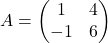 i
i 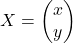 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- Els valors d’
 per als que l’equació matricial
per als que l’equació matricial 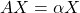 sols admet una solució. (4 punts)
sols admet una solució. (4 punts) - Totes les solucions de l’equació matricial
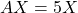 . (3 punts)
. (3 punts) - Comprovar que
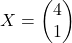 és una solució de l’equació matricial
és una solució de l’equació matricial 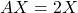 i, sense calcular la matriu
i, sense calcular la matriu 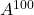 , obtenir el valor de
, obtenir el valor de 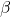 tal que
tal que 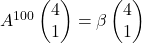 . (2 punts)
. (2 punts)
Juny 2019 – Problema 1.A.
Es donen la matriu 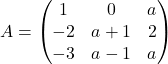 , que depèn del paràmetre
, que depèn del paràmetre  , i una matriu quadrada
, i una matriu quadrada  d’ordre 3 tal que
d’ordre 3 tal que 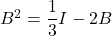 sent
sent 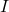 la matriu identitat d’ordre 3. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
la matriu identitat d’ordre 3. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
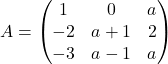 , que depèn del paràmetre
, que depèn del paràmetre - El rang de la matriu
 en funció del paràmetre
en funció del paràmetre  i el determinant de la matriu
i el determinant de la matriu 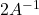 quan
quan 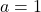 . (2+2 punts)
. (2+2 punts) - Totes les solucions del sistema d’equacions
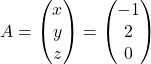 quan
quan 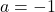 . (3 punts)
. (3 punts) - La comprovació de que
 és invertible, trobant
és invertible, trobant 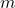 i
i 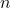 tals que
tals que 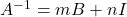 . (3 punts)
. (3 punts)