Problema 1
Donat el sistema d’equacions 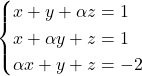 , sent
, sent  un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
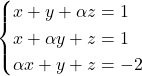 , sent
, sent - L’estudi del sistema en funció del paràmetre
 . (5 punts)
. (5 punts) - Les solucions del sistema quan
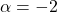 . (3 punts)
. (3 punts) - La solució del sistema quan
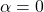 . (2 punts)
. (2 punts)
Problema 2
Siga la recta 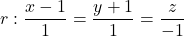 i els punts
i els punts 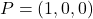 i
i 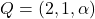 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El valor d’
 per a que la recta que passa
per a que la recta que passa 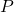 i
i 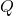 siga paral·lela a
siga paral·lela a  . (3 punts)
. (3 punts) - L’equació del pla que conté a
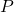 i
i 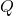 i és paral·lel a
i és paral·lel a  , quan
, quan 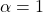 . (3 punts)
. (3 punts) - La distància del punt
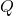 al pla que passa per
al pla que passa per 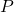 i és perpendicular a
i és perpendicular a  , quan
, quan 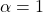 . (4 punts)
. (4 punts)
Encara no disponible
Problema 3
Es dona la funció real 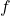 definida per
definida per 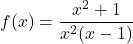 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El domini i les assímptotes de la funció
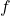 . (3 punts)
. (3 punts) - La integral
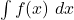 , així com la primitiva de
, així com la primitiva de 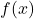 la gràfica de la qual passa pel punt
la gràfica de la qual passa pel punt 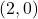 . (3+1 punts)
. (3+1 punts) - L’àrea de la regió limitada per la corba
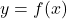 i les rectes
i les rectes 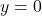 ,
, 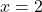 i
i 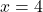 . (3 punts)
. (3 punts)
Encara no disponible
Problema 4
Es donen les matrius 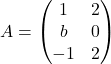 i
i 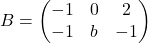 , que depenen del paràmetre real
, que depenen del paràmetre real 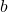 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
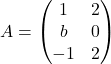 i
i - Els valors de
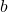 per a que cadascuna de les matrius
per a que cadascuna de les matrius 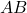 i
i 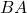 tinguen inversa. (3 punts)
tinguen inversa. (3 punts) - Els valors de
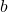 per a que la matriu
per a que la matriu 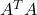 tinga inversa, sent
tinga inversa, sent 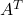 la matriu trasposta d’
la matriu trasposta d’ . (3 punts)
. (3 punts) - La inversa d’
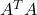 , quan aquesta inversa existisca. (4 punts)
, quan aquesta inversa existisca. (4 punts)
Problema 5
Es donen el pla  i els punts
i els punts 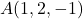 i
i 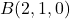 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- L’equació implícita del pla que passa pels punts
 i
i  i és perpendicular a
i és perpendicular a  . (4 punts)
. (4 punts) - Les equacions paramètriques de la recta
 que és perpendicular a
que és perpendicular a  i passa per
i passa per  . Troba dos plans els quals la seua intersecció siga la recta
. Troba dos plans els quals la seua intersecció siga la recta  . (1+2 punts)
. (1+2 punts) - La distància entre el punt
 i la recta
i la recta  . (3 punts)
. (3 punts)
Encara no disponible
Problema 6
En un triangle isòsceles, els dos costats iguals mesuren 10 centímetres cadascun . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- L’expressió de l’àrea
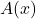 del triangle, en funció de la longitud
del triangle, en funció de la longitud 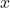 del tercer costat. (4 punts)
del tercer costat. (4 punts) - Els intervals de creixement i decreixement de la funció
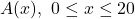 . (4 punts)
. (4 punts) - La longitud
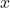 del tercer costat per a que l’àrea del triangle siga màxima i el valor d’aquesta àrea. (2 punts)
del tercer costat per a que l’àrea del triangle siga màxima i el valor d’aquesta àrea. (2 punts)
Encara no disponible