Juliol 2022 – Problema 1
Donat el sistema d’equacions 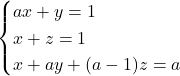 .
.
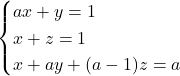 .
.- Discutir el sistema en funció del paràmetre real
 . (5 punts)
. (5 punts) - Trobar totes les solucions del sistema quan aquest siga compatible. (5 punts)
Juliol 2021 – Problema 1
Donat el sistema d’equacions 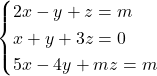 , on
, on 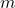 es un paràmetre real. Es demana:
es un paràmetre real. Es demana:
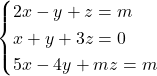 , on
, on - La discussió del sistema d’equacions en funció del paràmetre
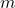 . (4 punts)
. (4 punts) - La solució del sistema quan
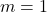 . (3 punts)
. (3 punts) - Les solucions del sistema quan aquest siga compatible indeterminat. (3 punts)
Juny 2021 – Problema 1
Donat el sistema d’equacions 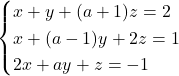 .
.
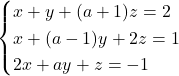 .
.- Estudieu-lo en funció dels valors del paràmetre real
 . (5 punts)
. (5 punts) - Trobeu totes les solucions del sistema quan aquest siga compatible. (5 punts)
Setembre 2020 – Problema 1
Donat el sistema d’equacions 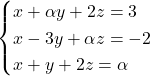 , on
, on  és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
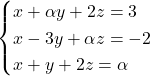 , on
, on - Els valors d’
 per als que el sistema és compatible. (4 punts)
per als que el sistema és compatible. (4 punts) - La solució del sistema quan
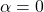 . (3 punts)
. (3 punts) - Les solucions del sistema en el cas que siga compatible indeterminat. (3 punts)
Juliol 2020 – Problema 1
Donat el sistema d’equacions 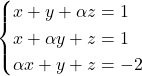 , sent
, sent  un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
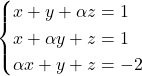 , sent
, sent - L’estudi del sistema en funció del paràmetre
 . (5 punts)
. (5 punts) - Les solucions del sistema quan
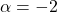 . (3 punts)
. (3 punts) - La solució del sistema quan
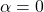 . (2 punts)
. (2 punts)
Juliol 2019 – Problema A.1.
Donat el sistema d’equacions 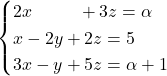 , sent
, sent  un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
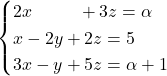 , sent
, sent - Els valors del paràmetre
 per als que el sistema es compatible i determinat. (4 punts)
per als que el sistema es compatible i determinat. (4 punts) - Les solucions del sistema quan
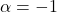 . (3 punts)
. (3 punts) - El valor d’
 per a que el sistema tinga una solució
per a que el sistema tinga una solució 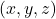 que verifique
que verifique 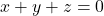 . (3 punts)
. (3 punts)
Juny 2019 – Problema B.1.
Es té el sistema d’equacions 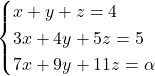 , on
, on  és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat
és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat
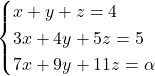 , on
, on - Els valors del paràmetre
 per als que el sistema és compatible i els valors d’
per als que el sistema és compatible i els valors d’ per als que el sistema és incompatible. (4 punts)
per als que el sistema és incompatible. (4 punts) - Totes les solucions del sistema quan siga compatible. (4 punts)
- La discussió de la compatibilitat i determinació del nou sistema deduït de l’anterior al canviar el coeficient 11 per qualsevol altre nombre diferent. (2 punts)