Opció A – Problema 1
Donat el sistema d’equacions 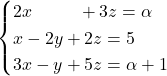 , sent
, sent  un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
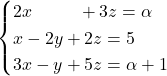 , sent
, sent - Els valors del paràmetre
 per als que el sistema es compatible i determinat. (4 punts)
per als que el sistema es compatible i determinat. (4 punts) - Les solucions del sistema quan
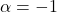 . (3 punts)
. (3 punts) - El valor d’
 per a que el sistema tinga una solució
per a que el sistema tinga una solució 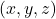 que verifique
que verifique 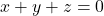 . (3 punts)
. (3 punts)
Opció A – Problema 2
Es tenen el pla 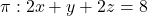 i el punt
i el punt 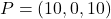 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La distància del punt
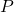 al pla
al pla  . (3 punts)
. (3 punts) - L’àrea del triangle el qual els seus vèrtexs són els punts
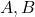 i
i 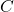 , obtinguts al trobar la intersecció del pla
, obtinguts al trobar la intersecció del pla  amb els eixos de coordenades. (4 punts)
amb els eixos de coordenades. (4 punts) - El volum del tetraedre el qual els seus vèrtexs són
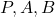 i
i 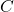 . (3 punts)
. (3 punts)
Encara no disponible.
Opció A – Problema 3
Es dona la funció real 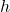 definida per
definida per 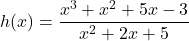 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El domini de la funció
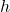 . Els límits
. Els límits 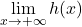 i
i 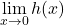 . (1+2 punts)
. (1+2 punts) - L’assímptota de la corba
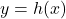 . (2 punts)
. (2 punts) - La primitiva de la funció
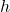 (és a dir,
(és a dir, 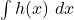 ) i l’àrea de la superfície tancada entre les rectes
) i l’àrea de la superfície tancada entre les rectes 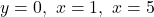 i la corba
i la corba 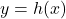 . (3+2 punts)
. (3+2 punts)
Opció B – Problema 1
Es donen les matrius 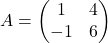 i
i 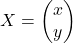 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- Els valors d’
 per als que l’equació matricial
per als que l’equació matricial 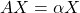 sols admet una solució. (4 punts)
sols admet una solució. (4 punts) - Totes les solucions de l’equació matricial
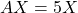 . (3 punts)
. (3 punts) - Comprovar que
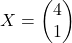 és una solució de l’equació matricial
és una solució de l’equació matricial 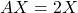 i, sense calcular la matriu
i, sense calcular la matriu 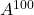 , obtenir el valor de
, obtenir el valor de 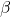 tal que
tal que 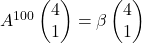 . (2 punts)
. (2 punts)
Opció B – Problema 2
Es donen en l’espai la recta 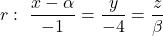 i el pla
i el pla 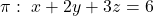 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La posició relativa de la recta
 y el pla
y el pla  en funció dels paràmetres reals
en funció dels paràmetres reals  i
i 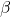 . (5 punts)
. (5 punts) - La distància entre la recta
 i el pla
i el pla  quan
quan 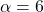 i
i 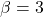 . (3 punts)
. (3 punts) - L’equació del pla que passa per
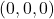 i que no talla al pla
i que no talla al pla  . (2 punts)
. (2 punts)
Encara no disponible.
Opció B – Problema 3
Un projectil està unit al punt 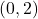 per una corda elàstica i tensa. El projectil recorre la corba
per una corda elàstica i tensa. El projectil recorre la corba 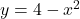 d’extrems
d’extrems 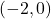 i
i 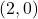 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La funció de la variable
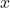 que expressa la distància entre un punt qualsevol
que expressa la distància entre un punt qualsevol 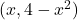 de la corba
de la corba 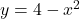 i el punt
i el punt 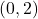 . (2 punts)
. (2 punts) - Els punts de la corba
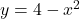 a major distància absoluta del punt
a major distància absoluta del punt 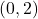 per a
per a 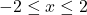 . (2 punts)
. (2 punts) - Els punts de la corba
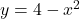 a menor distància absoluta del punt
a menor distància absoluta del punt 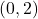 per a
per a 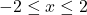 . (2 punts)
. (2 punts) - L’àrea de la superfície per la que s’ha menejat la corda elàstica, és a dir, l’àrea compresa entre les corbes
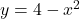 i
i 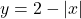 quan
quan 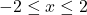 . (4 punts)
. (4 punts)