Problema 1
Donat el sistema d’equacions 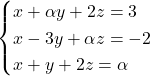 , on
, on  és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
és un paràmetre real. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
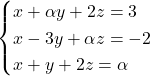 , on
, on - Els valors d’
 per als que el sistema és compatible. (4 punts)
per als que el sistema és compatible. (4 punts) - La solució del sistema quan
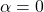 . (3 punts)
. (3 punts) - Les solucions del sistema en el cas que siga compatible indeterminat. (3 punts)
Problema 2
Es donen els plans 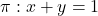 ,
, 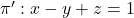 i el punt
i el punt 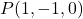 .Obtín raonadament, escrivint tots els passos del raonament utilitzat:
.Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- Unes equacions paramètriques de la recta
 que passa pel punt
que passa pel punt 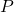 i és paral·lela als plans
i és paral·lela als plans  i
i 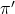 . (3 punts)
. (3 punts) - La distància de la recta
 als plans
als plans  i
i 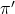 . (3 punts)
. (3 punts) - Les equacions de la recta que passa per
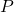 i talla perpendicularment a la recta obtinguda com intersecció dels plans
i talla perpendicularment a la recta obtinguda com intersecció dels plans  i
i 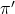 . (4 punts)
. (4 punts)
Problema 3
Donada la funció 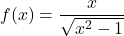 , obtín raonadament, escrivint tots els passos del raonament utilitzat:
, obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El domini de definició i les assímptotes de la funció
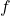 . (3 punts)
. (3 punts) - Els intervals de creixement i decreixement, així com la representació gràfica de la funció. (3 + 1 punts)
- El valor de
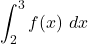 . (3 punts)
. (3 punts)
Problema 4
Siga 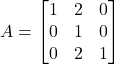 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
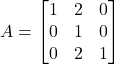 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:- La justificació de que
 té inversa i el càlcul de dita matriu inversa. (3 punts)
té inversa i el càlcul de dita matriu inversa. (3 punts) - Dos constants
 i
i 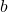 de manera que
de manera que 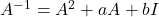 . Es pot utilitzar (sense comprovar-ho) que
. Es pot utilitzar (sense comprovar-ho) que  verifica que
verifica que 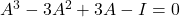 sent
sent 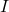 la matriu identitat. (3 punts)
la matriu identitat. (3 punts) - El valor de
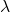 per a que el sistema d’equacions
per a que el sistema d’equacions 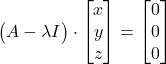 tinga infinites solucions. Per a dit valor de
tinga infinites solucions. Per a dit valor de 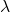 trobar totes les solucions del sistema. (2+2 punts)
trobar totes les solucions del sistema. (2+2 punts)
Problema 5
Es donen les rectes 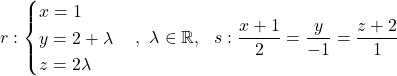 i el pla
i el pla 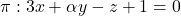 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
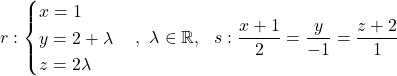 i el pla
i el pla - Si hi ha algun valor del paràmetre
 per al que la recta
per al que la recta  està continguda en el pla
està continguda en el pla  . (4 punts)
. (4 punts) - La distància entre les rectes
 i
i  . (3 punts)
. (3 punts) - El cosinus de l’angle que forma la recta
 i la recta
i la recta 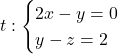 . (3 punts)
. (3 punts)
Encara no disponible
Problema 6
Els vèrtexs d’un triangle són 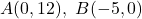 i
i 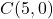 . Es desitja construir un rectangle inscrit en el triangle anterior, de costats paral·lels als eixos coordenats i dos dels dels seus vèrtexs tenen coordenades
. Es desitja construir un rectangle inscrit en el triangle anterior, de costats paral·lels als eixos coordenats i dos dels dels seus vèrtexs tenen coordenades 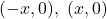 , on
, on 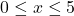 . Els altres dos vèrtexs estan situats als segments
. Els altres dos vèrtexs estan situats als segments 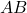 i
i 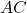 . Obtindre raonadament, escrivint tots els passos del raonament utilitzat:
. Obtindre raonadament, escrivint tots els passos del raonament utilitzat:
- L’expressió
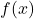 de l’àrea del rectangle anterior. (4 punts)
de l’àrea del rectangle anterior. (4 punts) - El valor d’
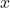 per al que l’àrea és màxima i les dimensions del rectangle obtingut. (3 punts)
per al que l’àrea és màxima i les dimensions del rectangle obtingut. (3 punts) - La proporció entre l’àrea del rectangle anterior i l’àrea del triangle. (3 punts)