Totes les respostes han d’estar degudament raonades.
Problema 1
Una agència immobiliària té tres locals en lloguer, pels quals ha cobrat en total 1.650 euros en aquest mes. L’agència ha pagat al propietari del primer local el 95% de la quantitat que ha cobrat pel lloguer; al propietari del segon local, el 90% de la
quantitat que ha cobrat pel lloguer; i al propietari del tercer local, el 80% de la quantitat cobrada pel lloguer. Després d’aquests tres pagaments, a l’agència li han quedat 132 euros de guany. Se sap també que el lloguer que es cobra pel pimer local
és el doble de la suma del que es cobra pel lloguer dels altres dos locals junts. Quants euros cobra l’agència per cadascun dels tres locals que té en lloguer?
(Plantejament correcte 5 punts – Resolució correcta 5 punts)
Problema 2
Una empresa apícola ven dos tipus de caixes amb tres varietats de mel en cadascuna: mel de romer, mel de flor del taronger i mel multifloral. La caixa de tipus A conté 2 pots de mel de romer, 2 de flor del taronger i 1 de multifloral. La caixa de tipus
B conté 1 pot de mel de romer, 2 de flor del taronger i 2 de multifloral. Cada dia l’empresa disposa de 280 pots de mel de romer, 300 de mel de flor del taronger i 250 de mel multifloral. Amb cada caixa de tipus A obté un benefici de 7 euros i amb
cada caixa de tipus B obté un benefici de 5 euros.
- Quantes caixes de cada tipus ha comercialitzar per a obtindre un benefici màxim? (8 punts)
- Quin és aquest benefici màxim? (2 punts)
Problema 3
Atesa la funció 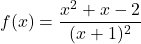 , es demana:
, es demana:
- El seu domini i els punts de tall amb els eixos coordenats. (2 punts)
- Les asímptotes horitzontals i verticals, si existeixen. (2 punts)
- Els intervals de creixement i decreixement. (2 punts)
- Els màxims i mínims locals, si existeixen. (2 punts)
- La representació gràfica de la funció a partir dels resultats anteriors. (2 punts)
Problema 4
En una empresa s’ha comprovat que els seus beneficis estan relacionats amb la seua inversió en publicitat segons la funció 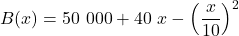 , en què
, en què 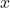 és la inversió en publicitat
és la inversió en publicitat 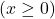 i
i 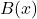 és el benefici obtingut, tots dos en euros.
és el benefici obtingut, tots dos en euros.
- Calculeu la quantitat invertida en publicitat que produeix un benefici màxim. Quin és aquest benefici màxim? (4 punts)
- Calculeu els intervals per a la inversió en publicitat en els quals els beneficis creixen o decreixen a mesura que s’inverteix en publicitat. (3 punts)
- Hi ha un valor per a la inversió en publicitat a partir del qual els beneficis obtinguts serien més baixos que si no s’invertira res en publicitat? En cas afirmatiu, determineu-ho. (3 punts)
Problema 5
Entre els clients d’una companyia d’assegurances d’automòbils, un 30% té menys de 30 anys, un 55% té entre 30 i 60 anys, i el 15% restant té més de 60 anys. Se sap que, entre els clients de menys de 30 anys, 3 de cada 4 no van presentar comunicat d’accident
l’any passat; entre els clients que tenen entre 30 i 60 anys, 9 de cada 10 no van presentar comunicat d’accident l’any passat; i entre els clients de més de 60 anys, 2 de cada 5 no van presentar comunicat d’accident l’any passat. Seleccionem a l’atzar
un client de la companyia.
- Anomenem
 el succés «el client seleccionat té més de 60 anys» i anomenem
el succés «el client seleccionat té més de 60 anys» i anomenem  el succés «el client seleccionat no va presentar comunicat d’accident l’any passat». Calculeu
el succés «el client seleccionat no va presentar comunicat d’accident l’any passat». Calculeu 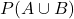 . (3 punts)
. (3 punts) - Anomenem
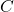 el succés «el client seleccionat té 30 anys o més» i anomenem
el succés «el client seleccionat té 30 anys o més» i anomenem 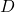 el succés «el client seleccionat va presentar comunicat d’accident l’any passat». Calculeu
el succés «el client seleccionat va presentar comunicat d’accident l’any passat». Calculeu 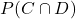 . (3 punts)
. (3 punts) - Si sabem que el client seleccionat va presentar comunicat d’accident l’any passat, calculeu la probabilitat que tinga 60 anys o menys. (4 punts)
Problema 6
En un joc es llancen dues monedes equilibrades i un dau de sis cares equilibrat. Un jugador guanya si obté dues cares i un nombre parell en el dau, o bé si obté exactament una cara i un nombre major o igual que cinc en el dau.
- Calculeu la probabilitat de que el jugador guanye. (2,5 punts)
- Si se sap que ha guanyat, quina és la probabilitat que obtinguera dues cares en llançar les monedes? (2,5 punts)
- Si se sap que ha guanyat, quina és la probabilitat que obtinguera un cinc en llançar el dau? (2,5 punts)
- Anomenem
 el succés «el jugador no guanya» i anomenem
el succés «el jugador no guanya» i anomenem  el succés «el jugador obté un sis en llançar el dau». Són independents els successos
el succés «el jugador obté un sis en llançar el dau». Són independents els successos  i
i  ? (2,5 punts)
? (2,5 punts)