En les respostes es deuen escriure tots els passos del raonament utilitzat.
Problema 1
Considerem les matrius 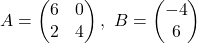 i
i 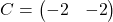 .
.
- Justifiqueu quines de les operacions següents es poden realitzar i efectueu les que siguen realitzables.
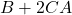 (1 punt)
(1 punt)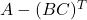 , en que la matriu
, en que la matriu 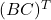 és la matriu transposada de
és la matriu transposada de 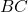 . (2 punts)
. (2 punts)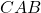 (2 punts)
(2 punts)
- Resoleu l’equació matricial
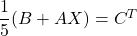 , en que
, en que 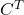 és la matriu transposada de
és la matriu transposada de 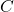 . (5 punts)
. (5 punts)
Problema 2
Un venedor disposa de cafè colombià i cafè brasiler, i amb ells realitza mescles que posa a la venda. Si mescla a parts iguals els dos tipus de cafè, obté una mescla que ven a 15 euros el quilo; si la proporció en la mescla és d’una part de cafè colombià
per tres parts de cafè brasiler, ven la mescla resultant a 10 euros el quilo. El venedor disposa de 100 quilos de cafè colombià i de 210 quilos de cafè brasiler. Vol fer les dues mescles de manera que els seus ingressos per venda siguen màxims.
- Calculeu quants quilos de cada mescla ha de produir per a obtindre l’ingrès màxim. (8 punts)
- Quin és aquest ingrès màxim? (2 punts)
Problema 3
Atesa la funció 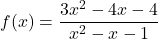 , es demana:
, es demana:
- El seu domini i els punts de tall amb els eixos coordenats. (2 punts)
- Les asímptotes horitzontals i verticals, si existeixen. (2 punts)
- Els intervals de creixement i decreixement. (2 punts)
- Els màxims i mínims locals, si existeixen. (2 punts)
- La representació gràfica de la funció a partir dels resultats anteriors. (2 punts)
Problema 4
Una màquina està productiva durant un any des de la seua compra. Se sap que el rendiment (en percentatge) que té la màquina 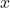 mesos després de la compra ve donat per la funció
mesos després de la compra ve donat per la funció 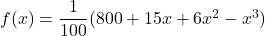 per a qualsevol valor
per a qualsevol valor 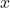 entre 0 i 12.
entre 0 i 12.
- És el rendiment que té la màquina un mes després de la compra superior al rendiment que té dos mesos després de la compra? (2 punts)
- Després de quants mesos després de la compra arriba la màquina al seu major rendiment?; quin és aquest rendiment màxim? (4 punts)
- Al llarg de l’any, té en algun moment la màquina un rendiment inferior al 10%? (4 punts)
Problema 5
Donats dos succesoss  i
i  , se sap que
, se sap que 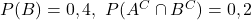 i
i 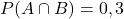 , en que
, en que 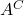 i
i 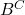 són els successos complementaris d’
són els successos complementaris d’ i
i  , respectivament. Es demana:
, respectivament. Es demana:
- Calcular la probabilitat del succés
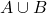 . (2,5 punts)
. (2,5 punts) - Calcular la probabilitat que solament es verifique un dels successos. (2,5 punts)
- Calcular la probabilitat de
 condicionat a
condicionat a  . (2,5 punts)
. (2,5 punts) - Són independents els successos
 i
i  ? (2,5 punts)
? (2,5 punts)
Problema 6
El director d’una entitat que audita la comptabilitat d’empreses sap, per experiències passades, que quan es fa una auditoria el 30% de les empreses mereix una qualificació «d’Excel·lent», el 50% de les empreses mereix la qualificació «d’Acceptable» i
el 20% restant mereix una qualificació de «Deficient». El director també sap que entre els auditors de la seua entitat hi ha un 90% d’auditors que sempre auditen correctament i donen a cada empresa la qualificació que mereix; però hi ha un 10% d’auditors
que no auditen correctament i donen sempre una qualificació «d’Acceptable».
- Quina proporció d’empreses auditades per aquesta entitat rep la qualificació de «Deficient»? (3 punts)
- Quina proporció d’empreses auditades per aquesta entitat rep la qualificació que realment mereix? (3 punts)
- Per a analitzar si un determinat auditor audita correctament o no, el director li encarrega que audite la comptabilitat d’una empresa triada a l’atzar. No sabem quina és la qualificació que es mereix l’empresa. Si l’auditor dona la qualificació
«d’Acceptable», quina és la probabilitat que aquest auditor siga un dels quals sempre auditen correctament? (4 punts)