Juliol 2022 – Problema 3
Donats els punts 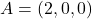 i
i 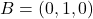 , i la recta
, i la recta 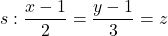 :
:
- Trobar l’equació de la recta
 que passa pels punts
que passa pels punts  i
i  . (2 punts)
. (2 punts) - Determinar l’equació implícita del pla que conté a la recta
 i és paral·lel a la recta
i és paral·lel a la recta  . (4 punts)
. (4 punts) - Calcular la distància del punt
 a la recta
a la recta  . (4 punts)
. (4 punts)
Encara no disponible.
Juliol 2022 – Problema 4
Donats els punts 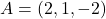 i
i 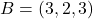 , i el pla
, i el pla  definit per
definit per 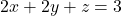 , obtindre:
, obtindre:
- El punt de tall
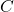 entre el pla
entre el pla  i la recta perpendicular a
i la recta perpendicular a  que passa per
que passa per  . (5 punts)
. (5 punts) - L’àrea del triangle que té per vèrtexs els punts
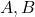 i
i 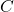 . (5 punts)
. (5 punts)
Encara no disponible.
Juny 2022 – Problema 3
Donades les rectes 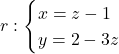 i
i 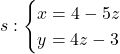 , es demana:
, es demana:
Donades les rectes 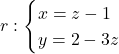 i
i 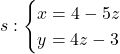 , es demana:
, es demana:
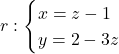 i
i 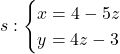 , es demana:
, es demana:- Indicar justificadament la posició relativa de
 i
i  . (5 punts)
. (5 punts) - Trobar l’equació de la recta
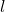 que passa per l’origen i talla a
que passa per l’origen i talla a  i
i  . (5 punts)
. (5 punts)
Encara no disponible.
Juny 2022 – Problema 4
Donats els plans 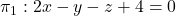 i
i 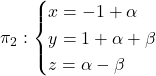 , i la recta
, i la recta 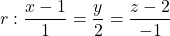 . Es demana:
. Es demana:
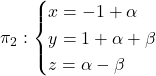 , i la recta
, i la recta - Calcular la posició relativa de
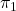 i
i 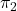 . (3 punts)
. (3 punts) - Calcular el punt
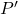 que és simètric al punt
que és simètric al punt 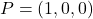 respecte del pla
respecte del pla 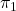 . (4 punts)
. (4 punts) - Calcular, si existeix, el punt d’intersecció de
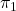 i
i  . (3 punts)
. (3 punts)
Encara no disponible.
Juliol 2021 – Problema 2
Es donen les rectes 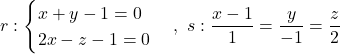 i el pla
i el pla 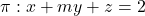 que depén del paràmetre real
que depén del paràmetre real 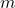 . Es demana:
. Es demana:
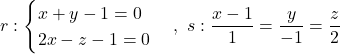 i el pla
i el pla - La posició relativa de les rectes
 i
i  . (4 punts)
. (4 punts) - El valor del paràmetre
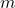 per a que la recta
per a que la recta  estiga continguda en el pla
estiga continguda en el pla  . (3 punts)
. (3 punts) - Els punts
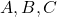 intersecció del pla
intersecció del pla  amb els eixos coordenats quan
amb els eixos coordenats quan 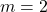 , així com el volum del tetraedre de vèrtexs
, així com el volum del tetraedre de vèrtexs 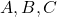 i
i 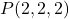 . (3 punts)
. (3 punts)
Encara no disponible.
Juliol 2021 – Problema 5
Donats els punts 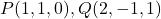 i
i 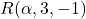 , es demana:
, es demana:
- L’equació del pla que conté a
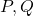 i
i 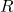 quan
quan 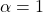 i la distància de dit pla a l’origen de coordenades. (3 punts)
i la distància de dit pla a l’origen de coordenades. (3 punts) - L’equació de la recta
 que passa per
que passa per 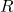 quan
quan 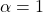 i és paral·lela a la recta
i és paral·lela a la recta  que passa per
que passa per 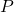 i
i 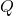 . Calculeu la distància entre les rectes
. Calculeu la distància entre les rectes  i
i  . (4 punts)
. (4 punts) - Els valors d’
 per als quals
per als quals 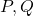 i
i 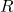 estan alineats i l’equació de la recta que els conté. (3 punts)
estan alineats i l’equació de la recta que els conté. (3 punts)
Encara no disponible.
Juny 2021 – Problema 2
Es donen els plans 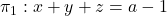 ,
, 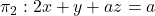 i
i 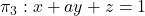 .
.
- Determineu la posició relativa dels tres plans en funció del paràmetre
 . (4 punts)
. (4 punts) - Per a
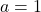 , calculeu, si existeix, la recta de tall entre els plans
, calculeu, si existeix, la recta de tall entre els plans 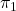 i
i 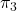 . (3 punts)
. (3 punts) - Per a
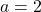 , calculeu, si existeix, la recta de tall entre els plans
, calculeu, si existeix, la recta de tall entre els plans 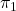 i
i 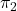 . (3 punts)
. (3 punts)
Encara no disponible.
Juny 2021 – Problema 5
Donats el punt 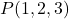 i el pla
i el pla 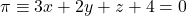 , es demana:
, es demana:
- Calculeu la distància del punt
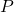 al pla
al pla  . (2 punts)
. (2 punts) - Calculeu el punt
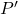 que és simètric del punt
que és simètric del punt 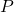 respecte del pla
respecte del pla  . (5 punts)
. (5 punts) - Calculeu l’equació del pla
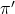 que passa per
que passa per 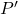 i és paral·lel a
i és paral·lel a  . (3 punts)
. (3 punts)
Encara no disponible.
Setembre 2020 – Problema 2
Es donen els plans 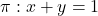 ,
, 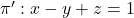 i el punt
i el punt 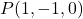 .Obtín raonadament, escrivint tots els passos del raonament utilitzat:
.Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- Unes equacions paramètriques de la recta
 que passa pel punt
que passa pel punt 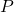 i és paral·lela als plans
i és paral·lela als plans  i
i 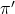 . (3 punts)
. (3 punts) - La distància de la recta
 als plans
als plans  i
i 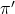 . (3 punts)
. (3 punts) - Les equacions de la recta que passa per
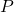 i talla perpendicularment a la recta obtinguda com intersecció dels plans
i talla perpendicularment a la recta obtinguda com intersecció dels plans  i
i 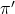 . (4 punts)
. (4 punts)
Setembre 2020 – Problema 5
Es donen les rectes 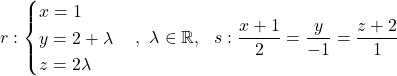 i el pla
i el pla 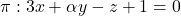 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
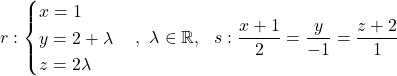 i el pla
i el pla - Si hi ha algun valor del paràmetre
 per al que la recta
per al que la recta  està continguda en el pla
està continguda en el pla  . (4 punts)
. (4 punts) - La distància entre les rectes
 i
i  . (3 punts)
. (3 punts) - El cosinus de l’angle que forma la recta
 i la recta
i la recta 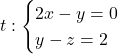 . (3 punts)
. (3 punts)
Encara no disponible.
Juliol 2020 – Problema 2
Siga la recta 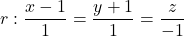 i els punts
i els punts 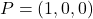 i
i 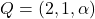 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El valor d’
 per a que la recta que passa
per a que la recta que passa 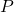 i
i 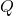 siga paral·lela a
siga paral·lela a  . (3 punts)
. (3 punts) - L’equació del pla que conté a
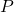 i
i 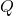 i és paral·lel a
i és paral·lel a  , quan
, quan 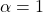 . (3 punts)
. (3 punts) - La distància del punt
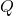 al pla que passa per
al pla que passa per 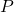 i és perpendicular a
i és perpendicular a  , quan
, quan 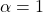 . (4 punts)
. (4 punts)
Encara no disponible.
Juliol 2020 – Problema 5
Es donen el pla  i els punts
i els punts 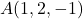 i
i 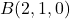 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- L’equació implícita del pla que passa pels punts
 i
i  i és perpendicular a
i és perpendicular a  . (4 punts)
. (4 punts) - Les equacions paramètriques de la recta
 que és perpendicular a
que és perpendicular a  i passa per
i passa per  . Troba dos plans els quals la seua intersecció siga la recta
. Troba dos plans els quals la seua intersecció siga la recta  . (1+2 punts)
. (1+2 punts) - La distància entre el punt
 i la recta
i la recta  . (3 punts)
. (3 punts)
Encara no disponible.
Juliol 2019 – Problema A.2.
Es tenen el pla 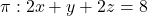 i el punt
i el punt 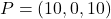 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La distància del punt
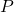 al pla
al pla  . (3 punts)
. (3 punts) - L’àrea del triangle el qual els seus vèrtexs són els punts
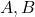 i
i 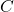 , obtinguts al trobar la intersecció del pla
, obtinguts al trobar la intersecció del pla  amb els eixos de coordenades. (4 punts)
amb els eixos de coordenades. (4 punts) - El volum del tetraedre el qual els seus vèrtexs són
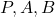 i
i 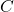 . (3 punts)
. (3 punts)
Encara no disponible.
Juliol 2019 – Problema B.2.
Es donen en l’espai la recta 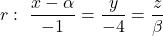 i el pla
i el pla 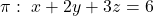 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- La posició relativa de la recta
 y el pla
y el pla  en funció dels paràmetres reals
en funció dels paràmetres reals  i
i 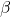 . (5 punts)
. (5 punts) - La distància entre la recta
 i el pla
i el pla  quan
quan 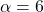 i
i 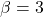 . (3 punts)
. (3 punts) - L’equació del pla que passa per
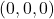 i que no talla al pla
i que no talla al pla  . (2 punts)
. (2 punts)
Encara no disponible.
Juny 2019 – Problema A.2.
Considerem en l’espai les rectes 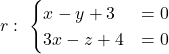 i
i 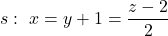 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
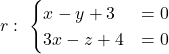 i
i - L’equació del pla que conté les rectes
 i
i  . (3 punts)
. (3 punts) - La recta que passa per
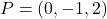 i talla perpendicularment a la recta
i talla perpendicularment a la recta  . (4 punts)
. (4 punts) - El valor que deuen tindre els paràmetres reals
 i
i 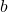 per a que la recta
per a que la recta  estiga continguda en el pla
estiga continguda en el pla 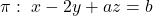 . (3 punts)
. (3 punts)
Juny 2019 – Problema B.2.
Siga  el pla d’equació
el pla d’equació 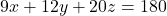 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- Les equacions dels dos plans paral·lels a
 que disten 4 unitats de
que disten 4 unitats de  . (4 punts)
. (4 punts) - Els punts
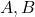 i
i 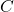 intersecció del pla
intersecció del pla  amb els eixos
amb els eixos 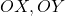 i
i 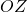 i l’angle que formen els vectors
i l’angle que formen els vectors 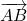 i
i 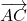 . (4 punts)
. (4 punts) - El volum del tetraedre el qual els seus vèrtexs són l’origen
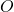 de coordenades i els punts
de coordenades i els punts 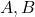 i
i 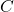 . (2 punts)
. (2 punts)
Encara no disponible.