Juliol 2022 – Problema 5
- Calcular, indicant tots els passos, la següent integral indefinida:
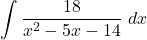 . (5 punts)
. (5 punts) - Determinar, en funció de
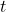 , el valor
, el valor 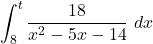 (2 punts)
(2 punts) - Determinar el valor de
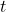 major que 8 per a que
major que 8 per a que 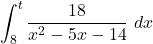 siga igual a
siga igual a 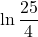 . (3 punts)
. (3 punts)
Juny 2022 – Problema 5
Considerem la funció 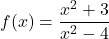 . Obtindre:
. Obtindre:
- El domini i els punts de tall amb els eixos. (1 punt)
- Les assímptotes de la funció. (2 punts)
- Els intervals de creixement i decreixement, i els extrems. (3 punts)
- La primitiva de la funció
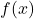 . (4 punts)
. (4 punts)
Juliol 2021 – Problema 3
Es considera la funció 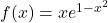 , calculeu:
, calculeu:
- El domini, els intervals de creixement i decreixement i els extrems relatius. (4 punts)
- Les assímptotes i la gràfica de
 . (3 punts)
. (3 punts) - La integral
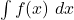 . (3 punts)
. (3 punts)
Juny 2021 – Problema 3
Considerem la funció 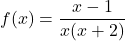 . Obtingau:
. Obtingau:
- El domini i les assímptotes de la funció. (2 punts)
- Els intervals de creixement i de decreixement de
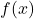 . (4 punts)
. (4 punts) - La integral
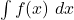 . (4 punts)
. (4 punts)
Setembre 2020 – Problema 3
Donada la funció 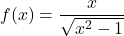 , obtín raonadament, escrivint tots els passos del raonament utilitzat:
, obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El domini de definició i les assímptotes de la funció
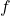 . (3 punts)
. (3 punts) - Els intervals de creixement i decreixement, així com la representació gràfica de la funció. (3 + 1 punts)
- El valor de
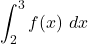 . (3 punts)
. (3 punts)
Juliol 2020 – Problema 3
Es dona la funció real 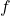 definida per
definida per 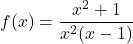 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El domini i les assímptotes de la funció
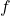 . (3 punts)
. (3 punts) - La integral
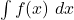 , així com la primitiva de
, així com la primitiva de 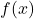 la gràfica de la qual passa pel punt
la gràfica de la qual passa pel punt 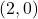 . (3+1 punts)
. (3+1 punts) - L’àrea de la regió limitada per la corba
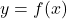 i les rectes
i les rectes 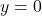 ,
, 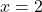 i
i 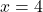 . (3 punts)
. (3 punts)
Encara no disponible.
Juliol 2019 – Problema A.3.
Es dona la funció real 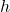 definida per
definida per 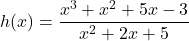 . Obtín raonadament, escrivint tots els passos del raonament utilitzat:
. Obtín raonadament, escrivint tots els passos del raonament utilitzat:
- El domini de la funció
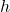 . Els límits
. Els límits 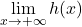 i
i 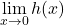 . (1+2 punts)
. (1+2 punts) - L’assímptota de la corba
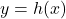 . (2 punts)
. (2 punts) - La primitiva de la funció
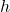 (és a dir,
(és a dir, 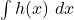 ) i l’àrea de la superfície tancada entre les rectes
) i l’àrea de la superfície tancada entre les rectes 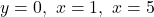 i la corba
i la corba 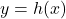 . (3+2 punts)
. (3+2 punts)
Juny 2019 – Problema A.3.
Es considera la funció 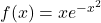 . Obtín raonadament, escrivint tots els passos del raonament utiltizat:
. Obtín raonadament, escrivint tots els passos del raonament utiltizat:
- Les assímptotes, els intervals de creixement i de decreixement, així com els màxims i mínims relatius de la funció
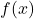 . (3 punts)
. (3 punts) - La representació gràfica de la corba
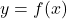 . (2 punts)
. (2 punts) - El valor del paràmetre
 per a que es puga aplicar el teorema de Rolle en l’interval
per a que es puga aplicar el teorema de Rolle en l’interval ![Rendered by QuickLaTeX.com [0,1]](https://matematiques.es/wp-content/ql-cache/quicklatex.com-25b6d943ab489c05a3dbd5ea29087a48_l3.png) a la funció
a la funció 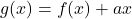 . (1 punt)
. (1 punt) - El valor de les integrals indefinides
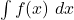 i
i 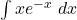 . (4 punts)
. (4 punts)