En les respostes es deuen escriure tots els passos del raonament utilitzat.
Problema 1
Donat el sistema d’equacions 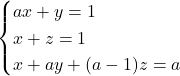 .
.
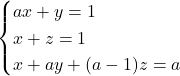 .
.- Discutir el sistema en funció del paràmetre real
 . (5 punts)
. (5 punts) - Trobar totes les solucions del sistema quan aquest siga compatible. (5 punts)
Problema 2
Donada la matriu 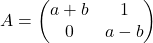 :
:
- Calcular els valors dels paràmetres
 i
i 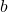 per a que es complisca que
per a que es complisca que 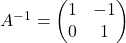 . (4 punts)
. (4 punts) - Per als valors d’
 i
i 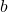 obtinguts en l’apartat anterior, calcular
obtinguts en l’apartat anterior, calcular 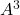 i
i 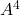 . (3 punts)
. (3 punts) - Calcular
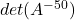 quan
quan 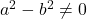 . (3 punts)
. (3 punts)
Problema 3
Donats els punts 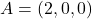 i
i 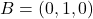 , i la recta
, i la recta 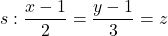 :
:
- Trobar l’equació de la recta
 que passa pels punts
que passa pels punts  i
i  . (2 punts)
. (2 punts) - Determinar l’equació implícita del pla que conté a la recta
 i és paral·lel a la recta
i és paral·lel a la recta  . (4 punts)
. (4 punts) - Calcular la distància del punt
 a la recta
a la recta  . (4 punts)
. (4 punts)
Encara no disponible.
Problema 4
Donats els punts 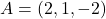 i
i 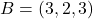 , i el pla
, i el pla  definit per
definit per 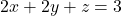 , obtindre:
, obtindre:
- El punt de tall
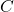 entre el pla
entre el pla  i la recta perpendicular a
i la recta perpendicular a  que passa per
que passa per  . (5 punts)
. (5 punts) - L’àrea del triangle que té per vèrtexs els punts
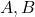 i
i 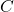 . (5 punts)
. (5 punts)
Encara no disponible.
Problema 5
- Calcular, indicant tots els passos, la següent integral indefinida:
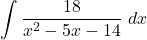 . (5 punts)
. (5 punts) - Determinar, en funció de
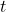 , el valor
, el valor 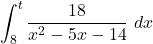 (2 punts)
(2 punts) - Determinar el valor de
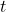 major que 8 per a que
major que 8 per a que 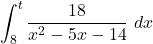 siga igual a
siga igual a 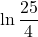 . (3 punts)
. (3 punts)
Problema 6
Considerar la funció 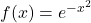 per als valors positius de
per als valors positius de 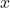 . Per cada punt
. Per cada punt 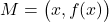 de la gràfica de
de la gràfica de 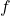 es tracen dues rectes paral·leles als eixos de coordenades
es tracen dues rectes paral·leles als eixos de coordenades 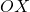 i
i 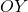 . Aquestes dues rectes, junt
amb els eixos de coordenades, defineixen un rectangle.
. Aquestes dues rectes, junt
amb els eixos de coordenades, defineixen un rectangle.
- Determinar l’àrea del rectàngle en funció de
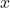 . (3 punts)
. (3 punts) - Trobar el punt
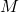 que proporciona major àrea i calcular aquesta àrea. (7 punts)
que proporciona major àrea i calcular aquesta àrea. (7 punts)