En les respostes es deuen escriure tots els passos del raonament utilitzat.
Problema 1
Donades les matrius 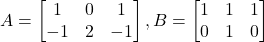 i
i 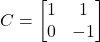 .
Es demana:
.
Es demana:
- Demostrar que
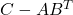 té inversa i calcular-la. (4 punts)
té inversa i calcular-la. (4 punts) - Calcular la matriu
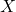 que verifica
que verifica 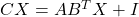 , on
, on 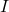 és la matriu identitat. (3 punts)
és la matriu identitat. (3 punts) - Justificar que
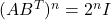 per a tot nombre natural
per a tot nombre natural 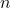 . (3 punts)
. (3 punts)
Problema 2
Donada la matriu 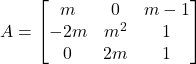 . Determinar:
. Determinar:
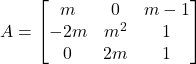 . Determinar:
. Determinar:- El rang de la matriu
 en funció del paràmetre real
en funció del paràmetre real 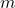 . (4 punts)
. (4 punts) - La matriu inversa d’
 en el cas
en el cas 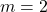 . (4 punts)
. (4 punts) - El nombre real
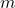 per al que el determinant de la matriu
per al que el determinant de la matriu 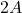 és igual a
és igual a 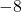 . (2 punts)
. (2 punts)
Problema 3
Donades les rectes 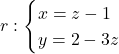 i
i 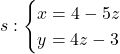 , es demana:
, es demana:
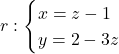 i
i 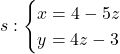 , es demana:
, es demana:- Indicar justificadament la posició relativa de
 i
i  . (5 punts)
. (5 punts) - Trobar l’equació de la recta
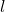 que passa per l’origen i talla a
que passa per l’origen i talla a  i
i  . (5 punts)
. (5 punts)
Encara no disponible.
Problema 4
Donats els plans 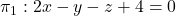 i
i 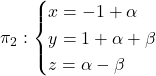 , i la recta
, i la recta 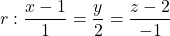 . Es demana:
. Es demana:
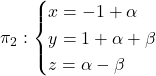 , i la recta
, i la recta - Calcular la posició relativa de
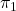 i
i 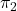 . (3 punts)
. (3 punts) - Calcular el punt
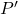 que és simètric al punt
que és simètric al punt 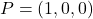 respecte del pla
respecte del pla 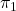 . (4 punts)
. (4 punts) - Calcular, si existeix, el punt d’intersecció de
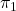 i
i  . (3 punts)
. (3 punts)
Encara no disponible.
Problema 5
Considerem la funció 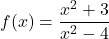 . Obtindre:
. Obtindre:
- El domini i els punts de tall amb els eixos. (1 punt)
- Les assímptotes de la funció. (2 punts)
- Els intervals de creixement i decreixement, i els extrems. (3 punts)
- La primitiva de la funció
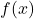 . (4 punts)
. (4 punts)
Problema 6
Es desitja construir un quadrat i un triangle equilàter tallant en dues parts un cable d’acer de 240 metres de longitud.
- Calcular la suma de les àrees del triangle i del quadrat en funció del valor
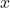 que correspon amb els metres que mesura un costat del triangle. (3 punts)
que correspon amb els metres que mesura un costat del triangle. (3 punts) - Calcular la longitud de cable necessària per a construir el triangle de manera que la suma de les àrees del triangle i del quadrat siga mínima i calcular l’àrea mínima. (7 punts)