En les respostes es deuen escriure tots els passos del raonament utilitzat.
Problema 1
Donat el sistema d’equacions 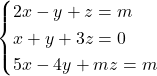 , on
, on  es un paràmetre real. Es demana:
es un paràmetre real. Es demana:
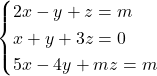 , on
, on - La discussió del sistema d’equacions en funció del paràmetre
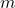 . (4 punts)
. (4 punts) - La solució del sistema quan
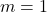 . (3 punts)
. (3 punts) - Les solucions del sistema quan aquest siga compatible indeterminat. (3 punts)
Problema 2
Es donen les rectes 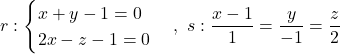 i el pla
i el pla 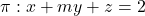 que depén del paràmetre real
que depén del paràmetre real 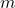 . Es demana:
. Es demana:
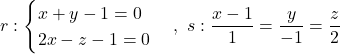 i el pla
i el pla - La posició relativa de les rectes
 i
i  . (4 punts)
. (4 punts) - El valor del paràmetre
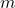 per a que la recta
per a que la recta  estiga continguda en el pla
estiga continguda en el pla  . (3 punts)
. (3 punts) - Els punts
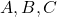 intersecció del pla
intersecció del pla  amb els eixos coordenats quan
amb els eixos coordenats quan 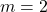 , així com el volum del tetraedre de vèrtexs
, així com el volum del tetraedre de vèrtexs 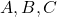 i
i 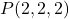 . (3 punts)
. (3 punts)
Encara no disponible.
Problema 3
Es considera la funció 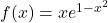 , calculeu:
, calculeu:
- El domini, els intervals de creixement i decreixement i els extrems relatius. (4 punts)
- Les assímptotes i la gràfica de
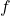 . (3 punts)
. (3 punts) - La integral
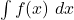 . (3 punts)
. (3 punts)
Problema 4
Es donen les matrius 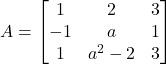 i
i 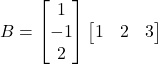 . Obtingau:
. Obtingau:
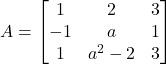 i
i  . Obtingau:
. Obtingau:- El rang de la matriu
 segons els valors del paràmetre
segons els valors del paràmetre  . (3 punts)
. (3 punts) - Una matriu
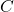 tal que
tal que 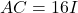 , sent
, sent 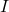 la matriu identitat, quan
la matriu identitat, quan 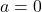 . (4 punts)
. (4 punts) - El rang de la matriu
 i la discussió de si el sistema
i la discussió de si el sistema  té solució. (3 punts)
té solució. (3 punts)
Problema 5
Donats els punts 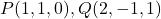 i
i 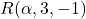 , es demana:
, es demana:
- L’equació del pla que conté a
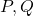 i
i 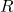 quan
quan 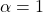 i la distància de dit pla a l’origen de coordenades. (3 punts)
i la distància de dit pla a l’origen de coordenades. (3 punts) - L’equació de la recta
 que passa per
que passa per 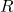 quan
quan 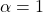 i és paral·lela a la recta
i és paral·lela a la recta  que passa per
que passa per 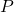 i
i 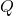 . Calculeu la distància entre les rectes
. Calculeu la distància entre les rectes  i
i  . (4 punts)
. (4 punts) - Els valors d’
 per als quals
per als quals 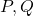 i
i 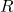 estan alineats i l’equació de la recta que els conté. (3 punts)
estan alineats i l’equació de la recta que els conté. (3 punts)
Encara no disponible.
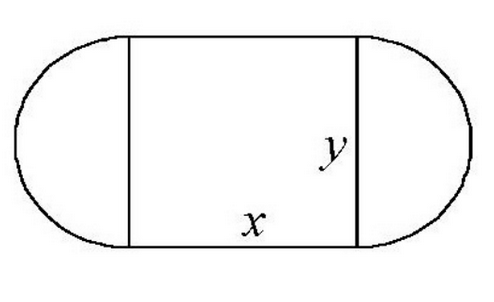
Problema 6
Volem dissenyar un camp de joc de manera que la part central siga rectangular, i les parts laterals siguen semicircumferències cap a fora. La superfície del camp mesura 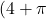 metres quadrats. Es volen pintar totes les ratlles de dit camp
tal i com es mostra en la figura. Es demana:
metres quadrats. Es volen pintar totes les ratlles de dit camp
tal i com es mostra en la figura. Es demana:
- Escriviu la longitud total de les ratlles del camp en funció de l’altura
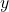 del rectangle. (5 punts)
del rectangle. (5 punts) - Calculeu les dimensions del camp per a que la pintura utilitzada siga mínima. (5 punts)